生命之光

如果你家墙上或者地面上铺了瓷砖，你可以仔细观察一下。别小瞧了这样一个不起眼的现象，它背后是数学领域中一个重要的概念，被称为“铺砌”。一直以来，很多数学家一直在研究，什么样的几何形状可以通过组合无缝隙地填满无限的平面。

铺砌可以分为周期性和非周期性铺砌。比如我们熟悉的三角形、正方形或者六边形，它们不断重复排列，就能周期性地铺砌二维空间。如果不限于二维平面，在三维空间中，立方体也可以实现周期性铺砌。

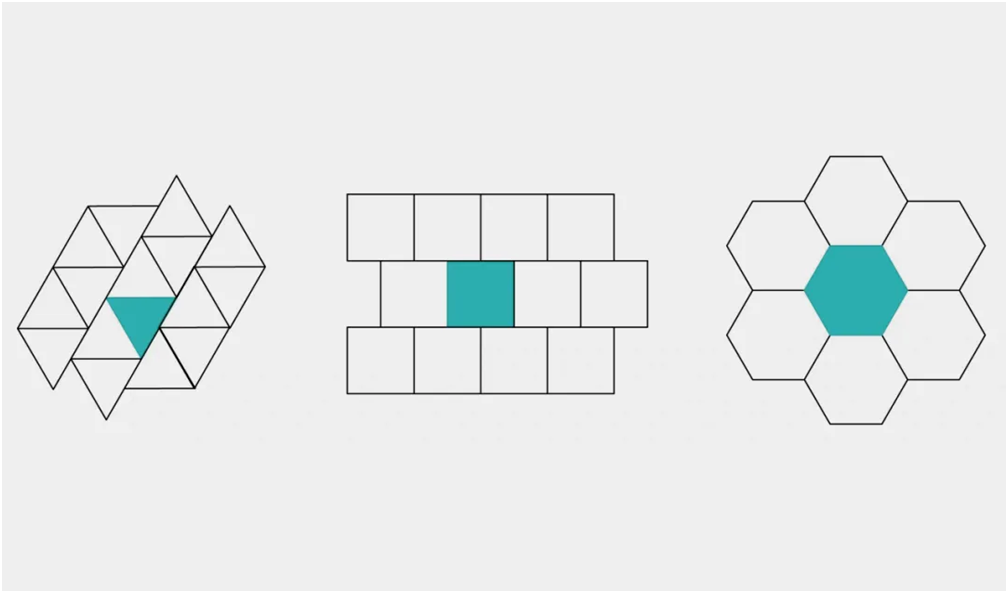
图1：三角形、正方形、六边形可以周期性地铺砌平面。

周期性铺砌的一大特点是，它的整体图案可以通过平移或者旋转重现出来。我们可以想象一张无限大的黑白格的国际象棋棋盘，如果把它向右再向下平移两格，移动过后的图案和原先完全一样。

图2：一个无限延伸的国际象棋棋盘，可以通过平移来获得完全一样的图案。

相比之下，非周期性铺砌就要复杂得多。因为它需要非重复性的排列，无论你怎么平移或者旋

转都无法重现原本的图案。数学家最初发现的非周期性铺砌由超过两万种形状组成。而最著名的一个例子叫作彭罗斯铺砌，罗杰·彭罗斯成功用两种不同的菱形实现了非周期性铺砌。

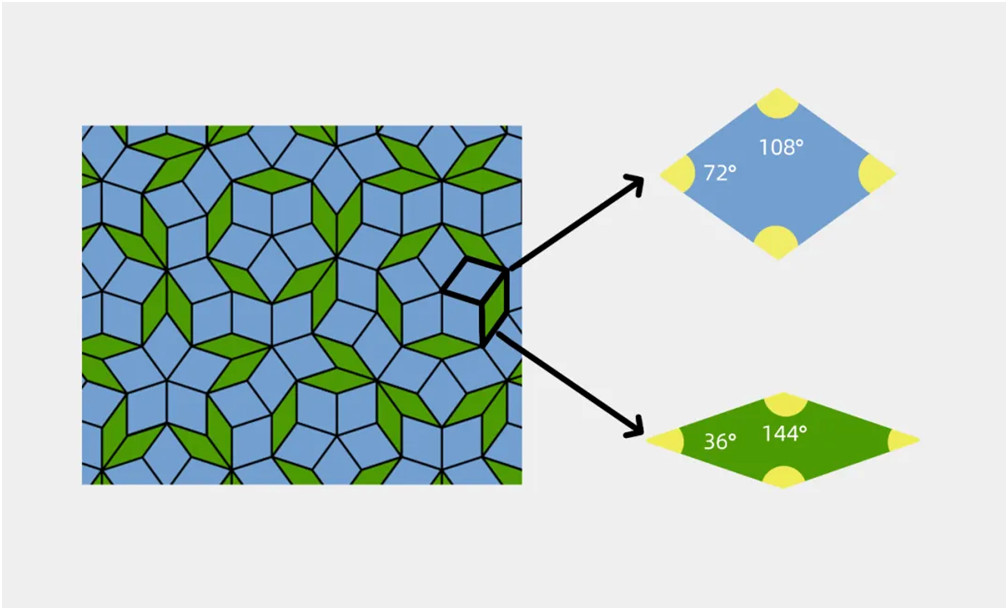
图3：由两种菱形组成的彭罗斯铺砌。

解决铺砌问题的典型思路是找到一些带拐角的形状进行拼接，就像二维平面中的三角形、正方形、六边形等等，这很符合直觉。如果让一些传统铺砌系统中形状的边弯曲，让拐角变“圆”时，这些被“软化”过的形状就没法不留缝隙地进行铺砌了。

然而，带拐角的形状在自然界中并不常见。最近，在一项发表在PNASNexus上的新研究中，数学家发现了一类新的形状，可以在没有任何拐角的情况下铺砌空间。这些新的几何形状带有圆角，他们将这些形状称为“软细胞”。

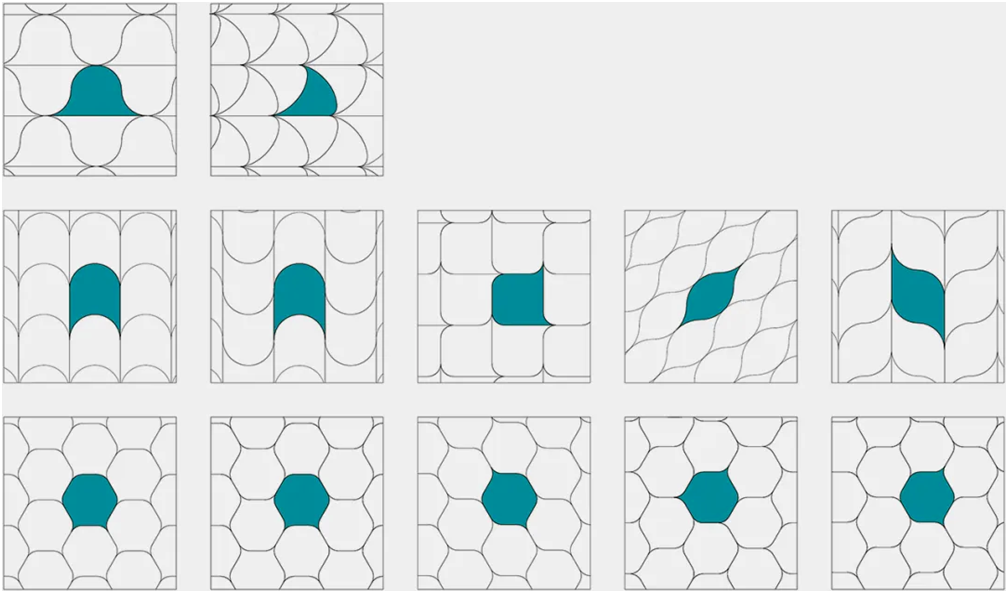
图4：新研究将一类新的可以无缝隙铺砌空间的形状命名为软细胞。第一行显示了等效于常规三角形的软铺砌，第二行显示了等效于长方形的软铺砌，第三行显示了等效于六边形的软铺砌。（图/Domokos et. al. / PNAS Nexus）

软细胞的特点是，这些形状在拐角数量最少的情况下能无缝隙铺砌空间。在二维空间里，所有软细胞都必须至少有两个“尖角”。而在三维空间中，软细胞变得更复杂但也更有趣了。它们竟然可以完全不带尖角，也能无缝隙地铺砌整个空间。

其实放眼自然界，这种形状的铺砌模式完全不是新鲜事儿。小到肌细胞和洋葱鳞茎的层，再到斑马条纹，甚至河流岛屿的形状，都有这样的铺砌模式。而一个最经典的软细胞铺砌的例子就是鹦鹉螺的壳室。从横截面来看，鹦鹉螺的壳室看起来像是有着两个尖角的二维软细胞，但实际上，在三维空间中，它的壳室没有任何拐角。

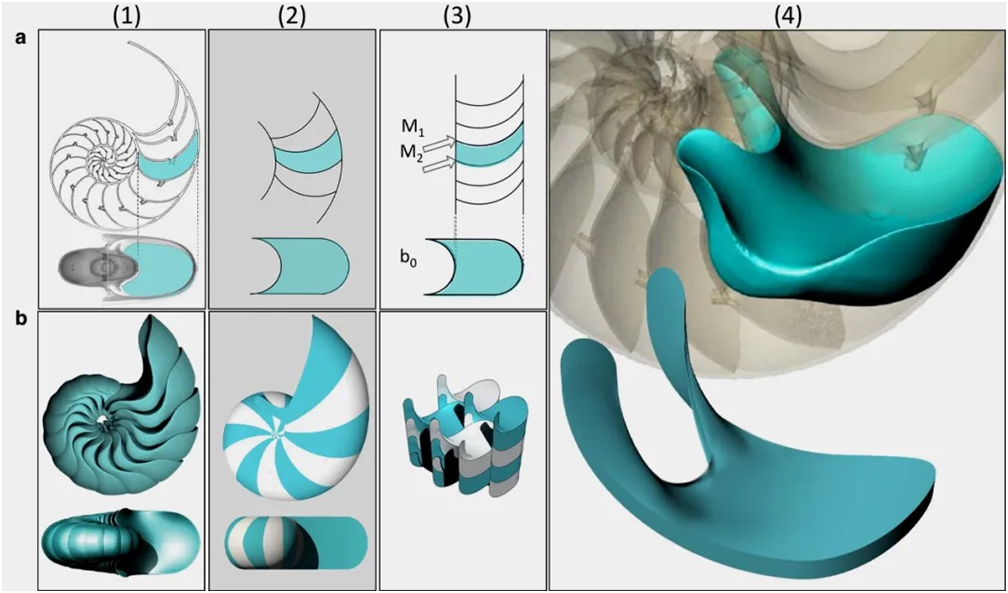
图5：鹦鹉螺腔室的几何形状。（图/Domokos et. al./ PNAS Nexus）

图6：软细胞拥有最小数量的尖角，并且能没有缝隙地铺砌空间。在自然界和建筑中都存在有着两个尖角的软细胞的例子。第1列显示的是几何软细胞示例，第2、3列显示的是自然界的软细胞示例，第4列显示的是建筑师扎哈·哈迪德的建筑设计。（图/Wikimedia Commons, Google Earth, Krisztina Regős.）

其实，当一些建筑师想要避免拐角时，他们也会凭直觉创造出这些形状，比如著名建筑师扎哈·哈迪德被称为“曲线女王”，她的设计就以大胆的曲线而闻名。这些建筑师在不知不觉中已经创造出了“软细胞”。

这项发现同样带来了几何学和生物学的一系列问题。目前，科学家还不清楚大自然究竟是如何利用这些“软”的形状来实现几何复杂性的。他们推测，自然通常会避免拐角，可能是因为拐角的扭折在形变能上的成本很高，也有可能会带来某些结构性的劣势。这可能是某种“自然的智慧”。

本文为科普中国·创作培育计划扶持作品

作者名称：沈雯

审核：刘歆 中国科学院数学与系统科学研究院 研究员

出品：中国科协科普部

监制：中国科学技术出版社有限公司、北京中科星河文化传媒有限公司

【我们尊重原创，也注重分享。版权原作者所有，如有侵犯您的权益请及时联系，我们将第一时间删除。分享内容不代表本网观点，仅供参考。】