科技博览

近期，流传着这样一条短视频——在液压机下万事万物仿佛都能被轻易地挤压、碾碎，从柔软的皮球到坚硬的钻石，只是花费的时间不同，液压机 “淡定”地碾碎着一切。

如果你身边有液压机，或者你曾经在视频中看到过液压机，那么你就会发现设备本身并不大，甚至还很轻便，但是这种“四两拨千斤”的效果就聚集在小小的仪器中。

是什么赋予了液压机力量？

其实，原理并不复杂，咱们依然先从简单的概念说起。

帕斯卡定律

不要一看这个原理初中没听说过，高中也没见过，就觉得很复杂。帕斯卡原理其实就出自流体静力学，在静止的液体中，由于液体的流动性，任何一点受到外力产生的效果，会瞬间且无损失地传递到流体的各点。

其中，在液压系统中通常会使用油或者水等液体来传导和放大力的作用，这是出于对物质微观排列的考虑。

3种微观粒子的空间排列

从图上可以清晰地看出来，液体和固体的微观粒子间隙都不大，但是要使室温中也能随意形变（流动），液体就是最好的状态了。同时液体分子间作用力很大，分子结合较为紧密，分子间距离始终保持稳定。

在流体静力学中，宏观上可认为液体的可压缩性非常小，基本可以忽略液体受力被压缩时的体积变化，因此，液体具有几乎完美的传导力天赋。

杠杆原理

我们将一整个液压系统拆分，先从杠杆原理入手，分步细致地讲解描述一下它的工作方式和物理原理。

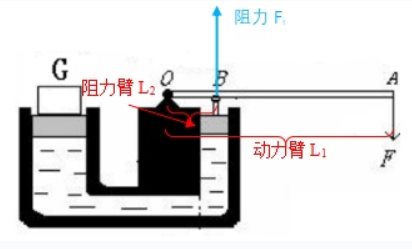
液压机的杠杆原理

首先，我们观察右半侧的图像，这是一个经典的杠杆结构，其中O为支点，F为动力，向上的F1为阻力，动力臂AO设为L1，阻力臂BO设为L2。

根据杠杆原理可知，动力×动力臂=阻力×阻力臂，即：F×L1=F1×L2

我们可以清晰地看到，当L1增大时，所需要的F就会变小，这样就可以省去一部分力量了。

压强公式

当然，单纯的杠杆原理并不足以解决问题，我们还需要讨论压强。

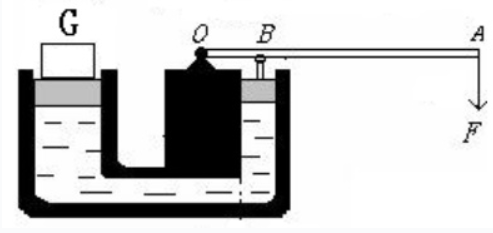
液压机

没错，还是这个图。这次我们观察图像的中心部分，左右两个活塞对水面都有正压力，故活塞和水面之间都有压强，我们记为P2和P1。

根据牛顿第三定律，右侧活塞对液体的压力与杠杆阻力F1是相互作用力，相互作用力大小相等、方向相反，故右侧活塞对液体的压力也记为F1，左侧液体对活塞的压力记为F2。

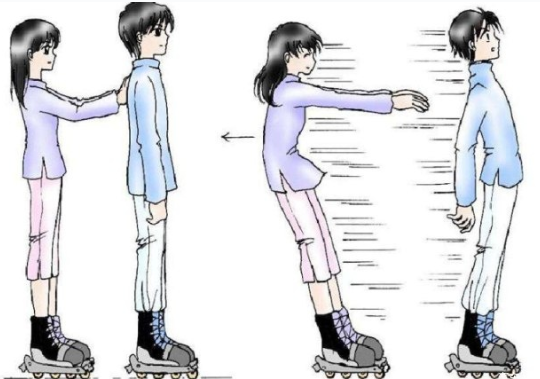
相互作用力大小相等、方向相反

此时的图像所代表的液压器受力如图：

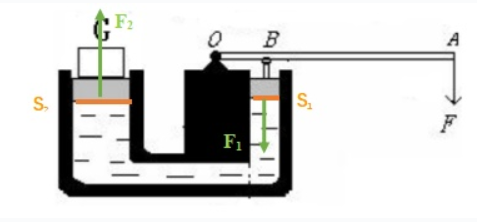
液压机的压强公式图

在文章的最开始我们说到，帕斯卡原理中力会通过流体无损失地传递到各点，即左右两液面所感受到的压强是一致的，P2 = P1。

根据压强公式，压强=压力/接触面积，即P=F÷S变式可得：F1÷S1=F2÷S2。因此，可以比较简单地推导出最终的结论：F1÷F2=S1÷S2（液压机要求S1<S2），可以发现，两个力之间的比例与两个液体的接触面积有关，即扩大接触面积的比例，就可以轻松地用很小的力量产生较大的力。

液压机的缺点

但是，液压机真的能如此完美吗？

那当然也不可能。由于液压机的基础原理是杠杆，必然就会出现省力但是费距离的情况，也就是说使用较小的力的时候，需要的位移就会比较大。例如我们在用千斤顶顶起车辆时，手臂下压的压力远小于车辆自身重力，然而手柄一端的距离总长度会远大于车辆升起的高度。

千斤顶原理（左侧为重物，升高缓慢，右侧为人工施力过程，施力幅度明显大于重物上升距离。）

生活应用

当然，生活中也有很多反向操作的例子。比如，打针的时候，人的力气是很大的，但是脆弱的血管并没有受到很大的冲击力，这是为什么呢？如果手边有针管的可以感受一下，将灌满水的针筒的针头去掉后，手指轻轻堵住出水口，用很大的力去推动活塞，手指也几乎感觉不到力。这就是因为接触面积的比例变了，现在是施力F1的接触面积大于F2的接触面积，如果还用刚才设定的符号来表示，应该是F1×S2÷S1=F2，自然F2的力量远小于F1。

生活中类似的应用还有很多，比如使用液力变矩器的汽车AT变速箱；汽车的刹车系统，通过液压系统将脚踩踏板的力放大使高速行驶的汽车进行制动等，都一一应用了液压机的原理。

现在明白了吗？物理并不复杂，这种“以小博大”的智慧你在生活中一定会用到的！

（审核专家：孟梦，中国科学院物理研究所，副研究员）

【我们尊重原创，也注重分享。版权原作者所有，如有侵犯您的权益请及时联系，我们将第一时间删除。分享内容不代表本网观点，仅供参考。】