科技博览
数字是很奇妙的存在,它们不仅被用作计算,某些数字本身就隐藏着很多特别的属性。

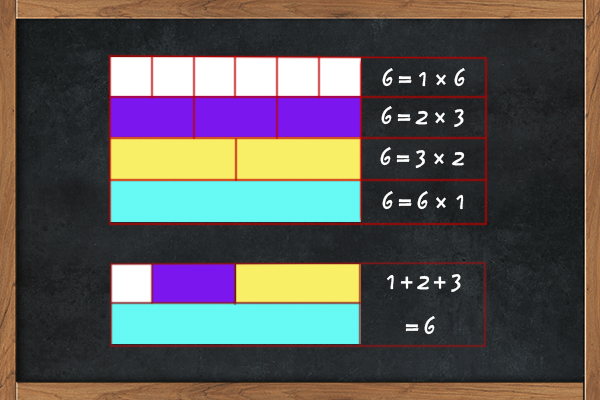
如果一个数恰好等于它的真因子(又叫“真因数”,即除了自身以外的约数)之和,则称该数为完全数,又称完美数或完备数。比如,6的约数为1、2、3、6,其真因子即为1、2、3,三者相加正好等于6,所以说6就是一个完全数。
最早研究完全数的是公元前6世纪的毕达哥拉斯,他发现了6和28的数字特性——两者都是完全数,并且他认为6这一完全数象征着“完满的婚姻、健康和美丽”。
除了完全数,根据自然数与其真因数之和的大小关系,还有盈数和亏数。以自然数“4”为例,它的真因数为1、2,两者相加等于3,小于它本身,这样的自然数叫做亏数。再以自然数“12”为例,它的真因数为1、2、3、4、6,相加之和等于16,大于它本身,这样的自然数叫做盈数。通过研究其规律,人们发现一个完全数的倍数一定是盈数,一个完全数的因子一定是亏数。
完全数在自然数中的占比较低,因此吸引了无数人加入到寻找完全数的行列。通过借助计算机,人们逐渐发现了越来越多的完全数,最大的一个在2013年被发现,位数高达4850340位。
数字6是被数学家发现的第一个完全数,第二个至第四个被发现的完全数依次为28、496、8128。这些数具有以下特点:
6=2×3=2×(22-1)
28=4×7=22×(23-1)
496=16×31=24×(25-1)
8128=64×127=26×(27-1)
由此出现了两个猜测:在n为质数时,所有2n-1(2n-1)形式的数都是完全数吗?所有偶完全数都属于2n-1(2n-1)这种形式吗?
这两个猜想得到了数学家的证实。最早研究了2n-1型的质数问题的是法国数学家梅森,因此这类数被称为梅森数,其中的质数n被称为梅森质数。梅森的研究表明,一个梅森质数对应一个偶完全数。目前通过计算机共发现了30多个梅森质数,但究竟还有多少,仍是一个未解之谜。对于是否存在奇完全数,目前尚未有结论,但数学家们已经证明:若奇完全数确实存在,这个数一定大于1050。
完全数是自然数中非常具有趣味性的一系列数字,相信未来会通过更加精准、先进的方式计算出更多的完全数。
本文由中国人民大学附属中学第二分校一级教师秦薇进行科学性把关。
本作品为“科普中国-科学原理一点通”原创。
【我们尊重原创,也注重分享。版权原作者所有,如有侵犯您的权益请及时联系,我们将第一时间删除。分享内容不代表本网观点,仅供参考。】

